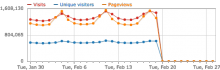
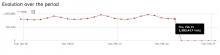
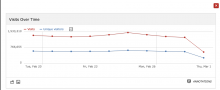
We don't see any iOS traffic data on Piwik since Feb 20, 2018, although real-time visitor data is still available.
Description
Event Timeline
Something is going on here yeah, i can see hits on apache log:
GET http://piwik.wikimedia.org/piwik.php?action_name=screen/Search&_viewts=1519861543&h=18&apiv=1&_idvc=776&url=http://Wikipedia/screen/Search&r=20822&_id=0e45035949b4098a&new_visit=1&s=42&_cvar=%7B%221%22:%5B%22Platform%22,%22iPhone10,5%22%5D,%222%22:%5B%22OS%20version%22,%2211.2.6%22%5D,%223%22:%5B%22App%20version%22,%221320%22%5D%7D&idsite=3&rec=1&m=45&_idts=1457729669&send_image=0&cdt=2018-02-28%2023:45:42&res=1242x2208 - text/html - WikipediaApp/5.7.5.1320 (iOS 11.2.6; Phone) en-ca -
Can @mforns that has the ops week this week take a look (cc @elukey)
There are plenty hits:
root@bohrium:/var/log/apache2# zcat other_vhosts_access.log.2.gz | grep -i iOs | wc -l
1104068
I wonder if the archive cron (which i think is running once a day) has not run due to machine failures for couple times and now it cannot run due to backlog of data. Maybe we need to setup crons per site once a day rather than having 1 cron processing all sites
Executed archiving by hand and got the following for website "3" which is iOS
INFO [2018-03-01 04:37:22] - Will invalidate archived reports for 2018-02-28 for following websites ids: 3 on
Executed the following:
elukey@bohrium:/var/log/piwik$
elukey@bohrium:/var/log/piwik$ for el in {20..28}; do sudo -u www-data /usr/share/piwik/console core:invalidate-report-data --dates=2018-02-$el --sites=3; done
Invalidating day periods in 2018-02-20 [segment = ]...
Invalidating week periods in 2018-02-20 [segment = ]...
Invalidating month periods in 2018-02-20 [segment = ]...
Invalidating year periods in 2018-02-20 [segment = ]...
Invalidating day periods in 2018-02-21 [segment = ]...
Invalidating week periods in 2018-02-21 [segment = ]...
Invalidating month periods in 2018-02-21 [segment = ]...
Invalidating year periods in 2018-02-21 [segment = ]...
Invalidating day periods in 2018-02-22 [segment = ]...
Invalidating week periods in 2018-02-22 [segment = ]...
Invalidating month periods in 2018-02-22 [segment = ]...
Invalidating year periods in 2018-02-22 [segment = ]...
Invalidating day periods in 2018-02-23 [segment = ]...
Invalidating week periods in 2018-02-23 [segment = ]...
Invalidating month periods in 2018-02-23 [segment = ]...
Invalidating year periods in 2018-02-23 [segment = ]...
Invalidating day periods in 2018-02-24 [segment = ]...
Invalidating week periods in 2018-02-24 [segment = ]...
Invalidating month periods in 2018-02-24 [segment = ]...
Invalidating year periods in 2018-02-24 [segment = ]...
Invalidating day periods in 2018-02-25 [segment = ]...
Invalidating week periods in 2018-02-25 [segment = ]...
Invalidating month periods in 2018-02-25 [segment = ]...
Invalidating year periods in 2018-02-25 [segment = ]...
Invalidating day periods in 2018-02-26 [segment = ]...
Invalidating week periods in 2018-02-26 [segment = ]...
Invalidating month periods in 2018-02-26 [segment = ]...
Invalidating year periods in 2018-02-26 [segment = ]...
Invalidating day periods in 2018-02-27 [segment = ]...
Invalidating week periods in 2018-02-27 [segment = ]...
Invalidating month periods in 2018-02-27 [segment = ]...
Invalidating year periods in 2018-02-27 [segment = ]...
Invalidating day periods in 2018-02-28 [segment = ]...
Invalidating week periods in 2018-02-28 [segment = ]...
Invalidating month periods in 2018-02-28 [segment = ]...
Invalidating year periods in 2018-02-28 [segment = ]...https://matomo.org/faq/how-to/faq_59/
Side note: now Piwik is called Matomo :)
Good news: Nuria was right, the archiver was adding missing data after invalidation.
Bad news: the extra IO (probably) triggered the Ganeti bug that causes the underlying host to freeze (bohrium, on which Piwik runs, is a Ganeti Virtual Machine) so I got only data up to the 22rd:
Added some documentation: https://wikitech.wikimedia.org/wiki/Analytics/Systems/Piwik#Invalidate_old_reports
Seems better now (archiver still running):
Super thanks @elikey. @chelsyx data shoudl be back but please have in mind that piwik is not a very reliable data store, nor does it have teh availability gurantees of eventlogging. It works well for small sites but IOs data is already pushing the limits.
Interesting stat: it took ~5h to archive the iOS data for the past week :D
Archived website id = 3, 4 API requests, Time elapsed: 19351.548s [2/12 done]
@JMinor, considering the unreliability of piwik, we should figure out a way with the Analytics team to back up the data, in case outage like this happen again.
Data is backed up, now, piwik is a tool mean to be used for low traffiqued sites, otherwise it just cannot handle it. In this case IOS data is getting too large. I think @JMinor is aware of this fact.
@Nuria I was talking about the outage on Nov 23 2017, which the data cannot be recovered. Is there any risk that this kind of outage happen again?
I invalidated the rest of the sites and run the archiver so all sites should be good now.