See parent task for context. Copying some bits of text from there:
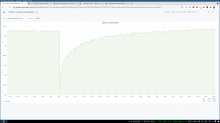
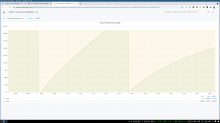
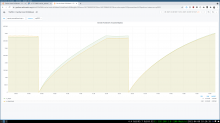
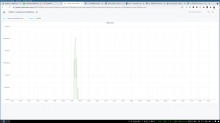
The current value of large_objects_cutoff is too small for commonly-linked images. This is not easily analyzed or fixed without looking at some other complex considerations about the total cache size, object size distributions, and varnish's eviction behavior and the ways it can fail, so we'll come back to this in more elsewhere in the ticket I think. The current temporary mitigation touches on this factor, but in a conservative and limited way.
[...]
large_objects_cutoff and all related things - the key thing that makes tuning this hard is varnish's nuke_limit, which caps the number of objects it will evict to make room for one new object (without any regard to relative sizes). If it can't make room within nuke_limit evictions, the request fails. If there's a large disparity in the minimum and maximum object sizes stored in the cache, large objects could commonly fail because there are too many small objects needing eviction to make room. Setting nuke_limit arbitrarily-large can also hurt (thrashing of cache contents for one-hit-wonder large objects, slow responses), and setting large_objects_cutoff much larger without a nuke_limit increase causes failures. The current eqsin-only mitigation is working, but it will fail to work for slightly-larger images than the last incident. We've also had some more-dynamic policies in the past based on T144187, where instead of having a fixed cutoff, the probability of the object entering the cache decreases as the size increases. This allows us to say something like "don't normally cache rare large objects, but do eventually cache them if they're popular enough". However, the tuning of the parameters for that are now quite outdated, and were also based purely on improving object and/or byte hit-rates, not surviving overwhelming events. The previous tuning gave near-zero probability of cache entry for the sizes in question in our recent scenarios. However, we could use a similar solution that's tuned for this problem rather than for hitrates, maybe (same exponential curve, but with admission probabilities that suit the cases we care about here...). I'm still digging into this.