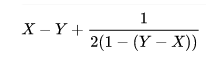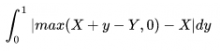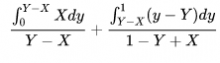How pt-heartbeat works:
Once every second (the cadence is important), the service updates a row in heartbeat.heartbeat table in the master and lets it replicate. Here are two examples of SQL commands issued:
REPLACE INTO `heartbeat`.`heartbeat` (ts, server_id, file, position, relay_master_log_file, exec_master_log_pos, shard, datacenter) VALUES ('2023-01-25T01:16:36.000820', '171966508', 'db1157-bin.002873', '1933994', NULL, NULL, 's3', 'eqiad') REPLACE INTO `heartbeat`.`heartbeat` (ts, server_id, file, position, relay_master_log_file, exec_master_log_pos, shard, datacenter) VALUES ('2023-01-25T01:16:37.000960', '171966508', 'db1157-bin.002873', '2268334', NULL, NULL, 's3', 'eqiad')
The timestamp, is the timestamp of SQL command (it's not using NOW() because then it would make it useless in SBR)
How mediawiki calculates the replication lag:
Now, when mediawiki wants to look up replication lag, it makes this query:
SELECT TIMESTAMPDIFF(MICROSECOND,ts,UTC_TIMESTAMP(6)) AS us_ago FROM heartbeat.heartbeat WHERE $where ORDER BY ts DESC LIMIT 1
This has so many issues:
- It's the time from the last heartbeat, not from the last landed query. e.g. if replag is 0.2 second (mostly replag is around this number), mw would report anything from 0.2s to 1.2s at random. That averages to half a second of error and that's why our internal db tools takes off 0.5s from the value (and max it with zero[1])
- We have repeatable read. If for whatever reason you read the value again, you might get an extremely large replag, I checked and couldn't find CONN_TRX_AUTOCOMMIT being used in getting replag (using that would be quite expensive)
- The timestamp of insert is based on the clock of the primary host, while the query checks the value is based on the clock of the replica. No two separate hosts have fully synchronized clocks. We could minimize it by buying atomic clocks and having a timeserver in each one of our datacenters (Google does it for some other distributed works) but doing it here feels like mowing your lawn with a tank.
- Given all the above, microsecond precision is completely unnecessary. Even with 0.5s removal, the replag values has error rate of five orders of magnitude bigger the microsecond precision.
[1] maxing with zero combined with the fact that most of the time replag is below 0.5 means if want to minimize the error in values you'd have to pick a different number than 0.5s, the math for it gets complicated and would require calculus of variation. I can try to do it but not sure if it's worth it specially given that any sort of calculation would require either assuming replag is a normal distribution between foo and bar which is a big assumption or collecting data and get some sense of its distribution but again, is it really worth it?
My suggestion to move forward: Reduce the precision to millisecond and remove 0.5s from the value (and max with zero).